Minimal mappings

The output of semantic matching is a mapping, namely a set of semantic correspondences between the two graphs in input. Among all possible mappings, the minimal mapping is an high quality mapping such that i) all the other correspondences can be computed from the ones in the minimal set in time linear in the size of the input graphs, and ii) none of the correspondences in the minimal set can be dropped without losing property i).

The main advantage of minimal mappings is that they are the minimal amount of information that needs to be dealt with. Notice that this is a rather important feature as the number of possible mappings can grow up to n x m with n and m the size of the two input ontologies. In particular, minimal mappings become crucial with large ontologies, for example, with web directories like DMOZ, where even relatively small subsets of the number of possible correspondences, potentially millions of them, are unmanageable.

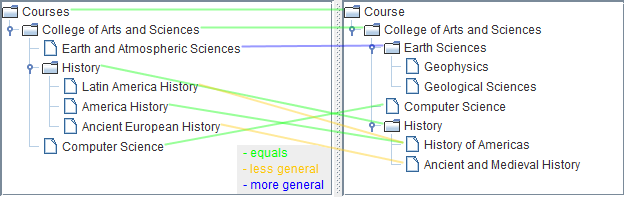
Figure 1: The set of minimal mappings when comparing two extracts of University course catalogs.

The output of the minimal mappings can be seen in Figure 1. Note how the set of mappings is smaller than the total number of possible mappings (n x m). This reduced set is more human-readable and in general correspond to what a person will expect to see as the result of the semantic matcher. A comparison of this minimal set with respect to the full set of mappings can be found in the Eaxmples and comparison page.

Minimal mappings provide clear usability advantages. Many systems and corresponding interfaces, mostly graphical, have been provided for the management of mappings but all of them hardly scale with the increasing number of nodes, and the resulting visualizations are rather messy, as witnessed by Pavel Shvaiko and Jérôme Euzenat in “Ten Challenges For Ontology Matching”. Furthermore, the maintenance of smaller mappings makes the work of the user much easier, faster and less error prone.

Formal definition of minimal and, dually, redundant mappings, evidence of the fact that the set of minimal mappings always exists and it is unique and an algorithm for computing them are presented by Fausto Giunchiglia, Vincenzo Maltese and Aliaksandr Autayeu in “Computing Minimal Mappings”.